Skip to main content

Probabilistic SHM under varying loads via the integration of data- and physics-based models

Students
Ahmad Amer
Parent Project
Structural Health Monitoring (SHM)

Motivation & Objectives

As with many machine learning techniques, the robustness and accuracy of GPRMs depend heavily on the availability of training data. This limits their capability of modelling the effects of varying conditions on the guided-wave signals simply because training data is not always available. This issue of data availability under varying operational and environmental conditions can, however, be solved using physics-based models. In this project, a framework was developed that promises the reduction in the training space of GPRMs along with the expansion of GPRM prediction capabilities to encompass damage size predictions under varying conditions. In addition, the proposed framework can also be used for filling the gap in the training space of multi-dimensional GPRMs as will be shown.

Main Contributions

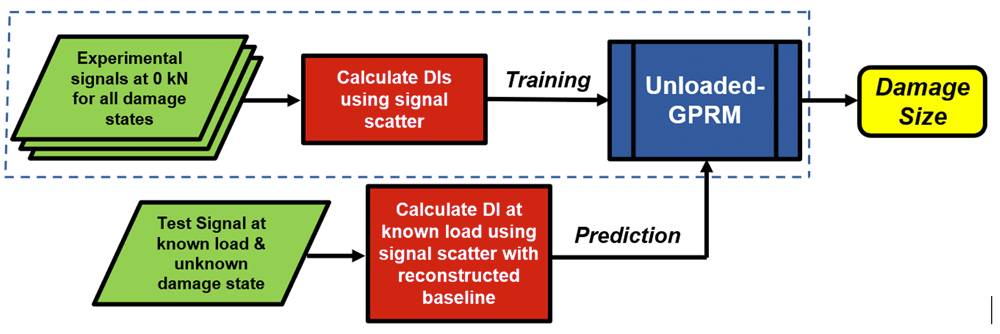
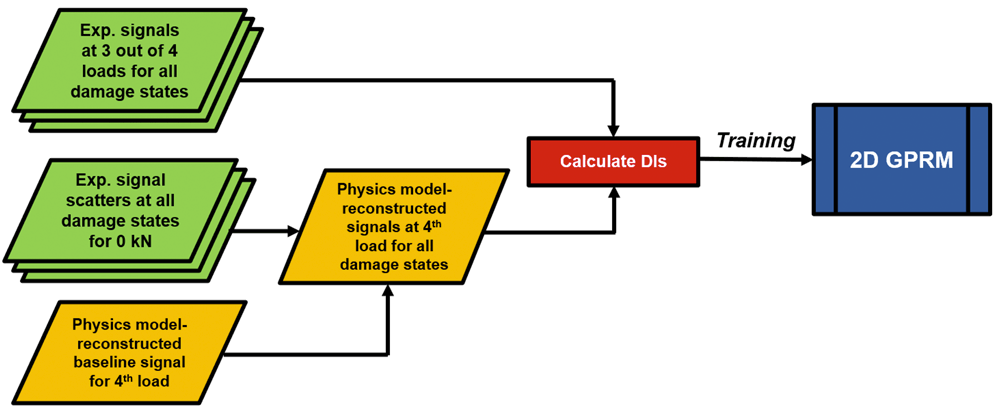
The major aim of this work is Integrating physics- and data-based models for accurate & robust damage identification under varying loading states. This framework attempts to solve two problems. The first one is the unavailability of experimental signals under load at varying damage states for training GPRMs that are robust to varying load states. Here the physics model-reconstructed signals are used in assisting one-dimensional GPRMs trained only using experimental data at zero load (and modelling DIs with damage size) in the prediction process by compensating the effects of load from incoming test DI points at unknown damage states. The second problem being tacked here is the unavailability of training data sets at a specific load for different damage sizes. Physics model-reconstructed signals are used here in filling the gap in the training space of two-dimensional GPRMs, which require the availability of experimental data at varying loads and damage sizes (and model DIs with damage size and load), by synthesizing signals for varying damage sizes at a specific load that is missing in the experimental training set.

Method of Approach

Two different approaches were developed in order to reach this goal. In the first approach, physics-based models are used for compensating the effects of load so that GPRMs trained with zero-load data can accurately quantify damage size. Given sensor data from unloaded component:

  • 1D GPRMs are trained at no-load conditions
  • Physics-based models are developed for synthesizing baseline signals at varying loads
  • Load effects are compensated from incoming test signals using model-reconstructed baselines
  • Damage is identified and quantification confidence bounds are extracted for proper decision-making

In the second approach, physics-based models were used in order to fill the gap in training data for properly training multi-dimensional GPRMs. Given sensor data under various loads:

  • “Missing” training data is synthesized at any load using physics-based models
  • Multi-dimensional GPRMs (load and damage size) are trained using mixed experimental & synthesized training sets
  • Damage & load states are identified and prediction confidence bounds are extracted

Figures 1 and 2 show the developed frameworks for the first and second approaches, respectively.

Indicative Results

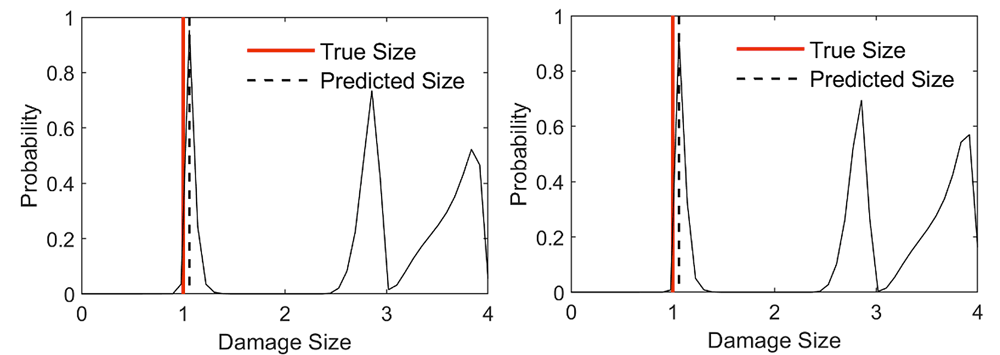
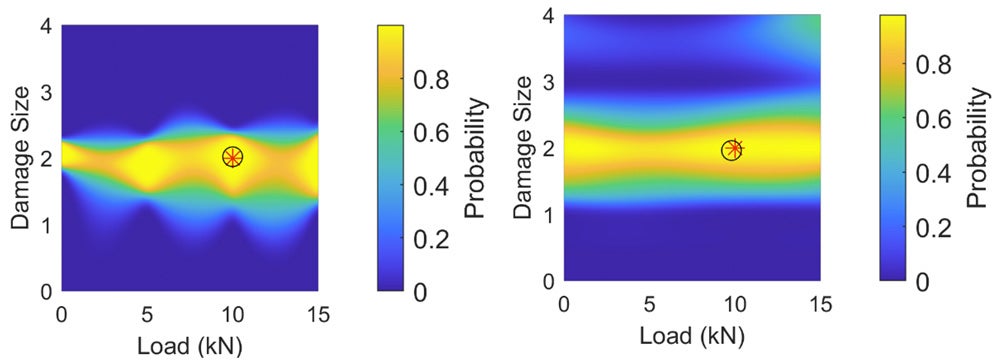
Figure 3 shows prediction probabilities using the first approach applied to 1D GPRMs, and Figure 4 shows the same from the second approach applied to 2D GPRMs
 

first approach
Figure 1. The method of approach for the first approach in the integration of physics- /data-based models for damage quantification applied to 1-dimensional problems.
second approach
Figure 2. The method of approach for the second approach in the integration of physics- /data-based models for damage quantification applied to 2-dimensional problems.
prediction probabilities from first approach
Figure 3. Indicative 1-state prediction probabilities from the first approach in the integration of physics- /data-based models for damage quantification from (left) experimentally-compensated test points and (right) physics model-compensated test points.
prediction probabilities from the second approach
Figure 4. Indicative 2-state prediction probabilities from the second approach in the integration of physics- /data-based models for damage quantification from (left) a model trained fully with experimental data sets and (right) a model trained with experimental and model-reconstructed data sets. The red asterisk indicates the actual state while the black circle indicates the predicted state.