Skip to main content

Data-driven stochastic identification of guided waves propagation under varying environmental and operating conditions

Students
Shabbir Ahmed
Parent Project
Data-driven stochastic modeling and identification

Objective

Active sensing acousto-ultrasound guided-wave based SHM techniques have shown great promise due to their potential sensitivity to small damages. However, the methods' robustness and diagnosis capability become limited in the presence of environmental and operational variability such as change in surrounding temperature, different load and boundary conditions, variation in material properties, etc. In addition, the currently used techniques rely on deterministic damage diagnosis schemes, rather than probabilistic frameworks which can account for uncertainty arising from different sources. As such, it is critical to model guided wave propagation in the presence of varying external sources, environments, operating conditions, and material property variations that impose uncertainty on guided wave propagation.

Motivation

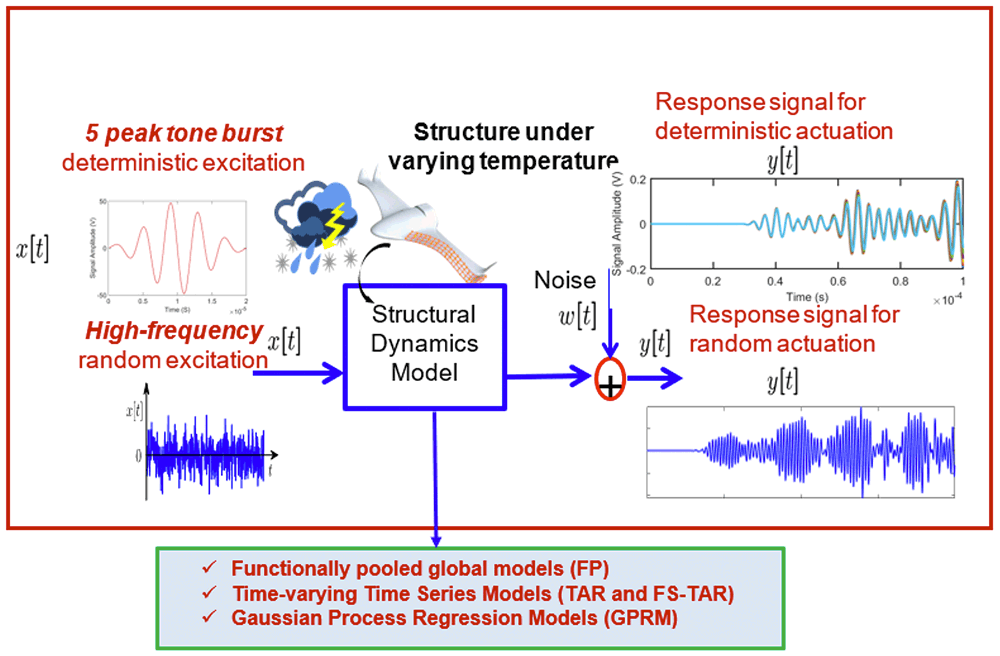
The motivation for my study is to model guided wave propagation under uncertainty in order to develop a robust SHM system and impart intelligence and awareness in smart structures. In order to do so, we have harnessed stochastic time series models, advanced statistics, stochastic signals and systems theory and more recently, machine learning or statistical learning tools such as gaussian process regression models.

We have investigated two types of systems.

  • Systems excited by narrow-band tone burst deterministic actuation
  • Systems excited by broadband high-frequency random actuation

Contributions

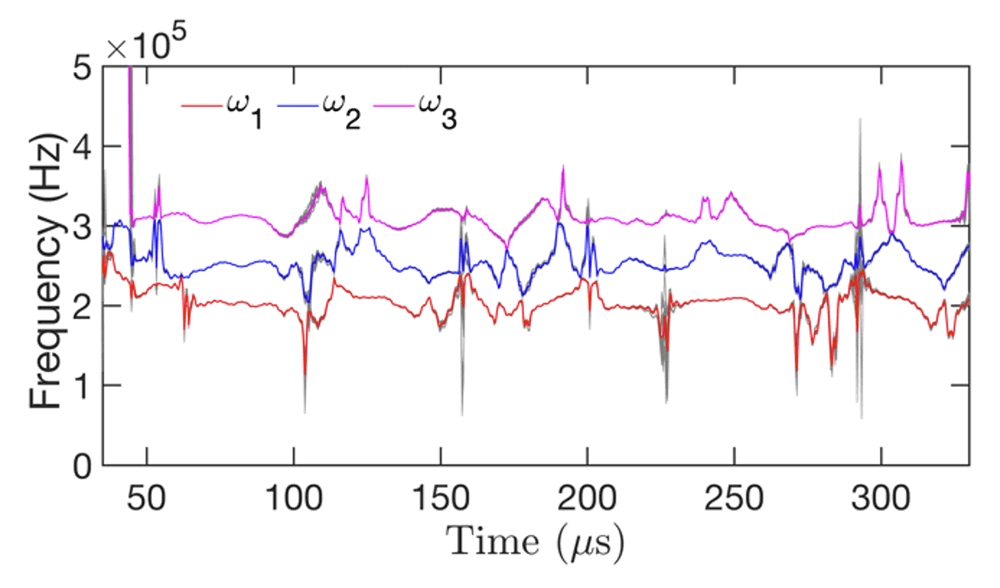
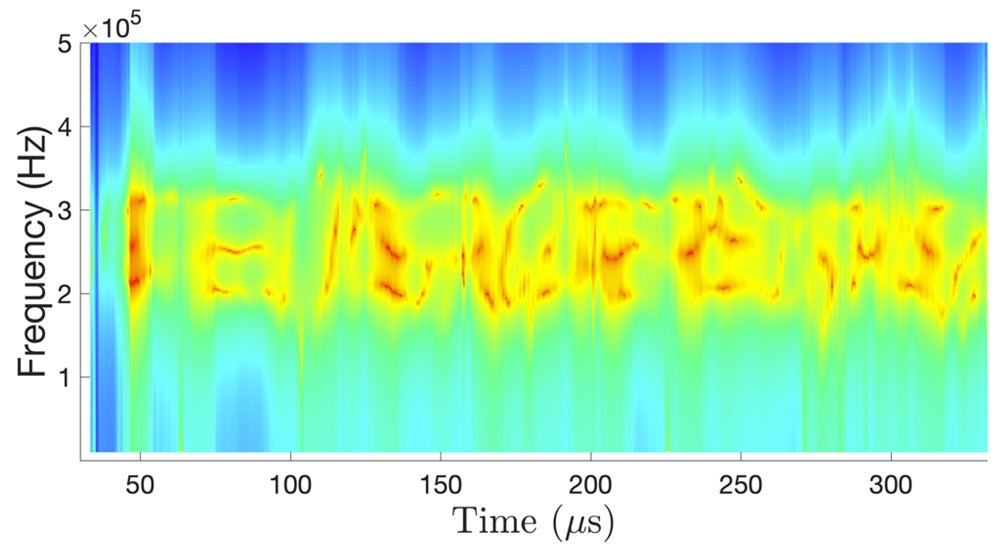
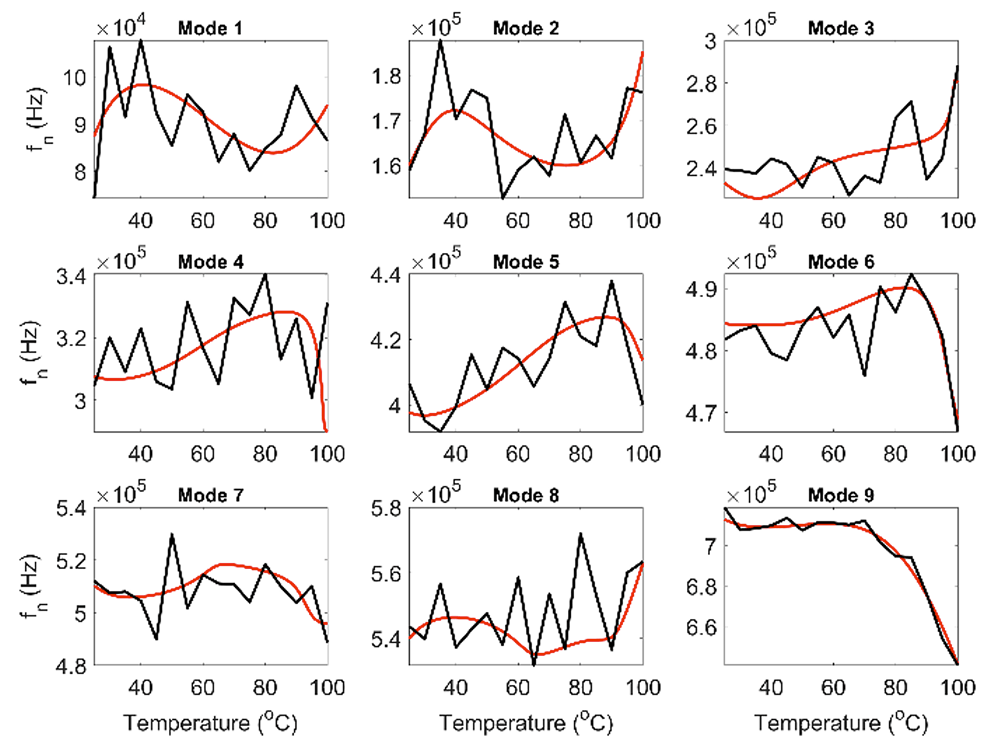
  • Identification of Guided wave propagation under temperature variation
  • Identification of Guided wave propagation under random actuation  
  • Surrogate modeling of guided wave propagation under uncertainty

Method of Approach

In order to generate data, we performed both experiments and finite-element modeling. We used deterministic tone-burst actuation as well as random gaussian white noise actuation for generating guided waves in thin aluminum plates subjected to different temperatures and loads. We then identified the system and modeled guided wave propagation using stochastic time-varying time series models and functionally pooled global models.

Schematic diagram
Figure 1: Schematic diagram for the identification of guided wave propagation under narrow band and random actuation
Time-varying natural frequencies
Figure 2: Time-varying natural frequencies extracted from the systems response signal with the help of stochastic time-varying time series models. The specific model that was chosen was time-varying autoregressive model with a model order 6 and a forgetting factor of 0.532, compactly written as RML-TAR(6)_0.532. As the model order is is 6, so there are three natural frequencies and damping ratios. As it is a recursive estimation, so the estimation accuracy at the beginning of time is not very good.
“frozen-time” frequency response function (FRF)
Figure 3: This figure shows the top view of the three dimensional “frozen-time” frequency response function (FRF) derived from parametric RML-TAR(6)_0.532 model. By comparing with figure 2, it can be observed that a very good match exists between the FRF and the system’s natural frequencies.
Natural frequencies of an aluminum plate
Figure 4. Natural frequencies of an aluminum plate fitted with piezo-electric actuators/sensors under varying temperature states obtained by a multitude of conventional auto-regressive models (black line, multi-model approach) and functionally pooled global models (red line). It can be observed that the natural frequencies obtained by functionally pooled global models are smooth functions of temperature and vary non-linearly. In fact, natural frequencies at any specific temperature within the range can be obtained with the help of this model.